Publications

2021

1. CES

   

   Calibrate, Emulate, Sample

   Cleary, Emmet, Garbuno-Inigo, Alfredo, Lan, Shiwei, Schneider, Tapio, and Stuart, Andrew M

   Journal of Computational Physics 2021

   Abs arXiv Bib

   Many parameter estimation problems arising in applications can be cast in the framework of Bayesian inversion. This allows not only for an estimate of the parameters, but also for the quantification of uncertainties in the estimates. Often in such problems the parameter-to-data map is very expensive to evaluate, and computing derivatives of the map, or derivative-adjoints, may not be feasible. Additionally, in many applications only noisy evaluations of the map may be available. We propose an approach to Bayesian inversion in such settings that builds on the derivative-free optimization capabilities of ensemble Kalman inversion methods. The overarching approach is to first use ensemble Kalman sampling (EKS) to calibrate the unknown parameters to fit the data; second, to use the output of the EKS to emulate the parameter-to-data map; third, to sample from an approximate Bayesian posterior distribution in which the parameter-to-data map is replaced by its emulator. This results in a principled approach to approximate Bayesian inference that requires only a small number of evaluations of the (possibly noisy approximation of the) parameter-to-data map. It does not require derivatives of this map, but instead leverages the documented power of ensemble Kalman methods. Furthermore, the EKS has the desirable property that it evolves the parameter ensemble towards the regions in which the bulk of the parameter posterior mass is located, thereby locating them well for the emulation phase of the methodology. In essence, the EKS methodology provides a cheap solution to the design problem of where to place points in parameter space to efficiently train an emulator of the parameter-to-data map for the purposes of Bayesian inversion.

   @article{Cleary2021,
     author = {Cleary, Emmet and Garbuno-Inigo, Alfredo and Lan, Shiwei and Schneider, Tapio and Stuart, Andrew M},
     title = {Calibrate, Emulate, Sample},
     journal = {Journal of Computational Physics},
     volume = {424},
     year = {2021},
     image = {/assets/img/pubimg/ces-fmk.png},
     url = {https://doi.org/10.1016/j.jcp.2020.109716},
     abbr = {CES},
     bibtex_show = {true},
     publisher = {Elsevier},
     selected = {true},
     arxiv = {2001.03689}
   }

2020

1. Affine Invariant Interacting Langevin Dynamics for Bayesian Inference

   Garbuno-Inigo, Alfredo, Nüsken, Nikolas, and Reich, Sebastian

   SIAM Journal on Applied Dynamical Systems 2020

   Abs arXiv Bib

   We propose a computational method (with acronym ALDI) for sampling from a given target distribution based on first-order (overdamped) Langevin dynamics which satisfies the property of affine invariance. The central idea of ALDI is to run an ensemble of particles with their empirical covariance serving as a preconditioner for their underlying Langevin dynamics. ALDI does not require taking the inverse or square root of the empirical covariance matrix, which enables application to high-dimensional sampling problems. The theoretical properties of ALDI are studied in terms of nondegeneracy and ergodicity. Furthermore, we study its connections to diffusion on Riemannian manifolds and Wasserstein gradient flows. Bayesian inference serves as a main application area for ALDI. In case of a forward problem with additive Gaussian measurement errors, ALDI allows for a gradient-free approximation in the spirit of the ensemble Kalman filter. A computational comparison between gradient-free and gradient-based ALDI is provided for a PDE constrained Bayesian inverse problem.

   @article{Garbuno-Inigo2020,
     author = {Garbuno-Inigo, Alfredo and N{\"u}sken, Nikolas and Reich, Sebastian},
     title = {Affine Invariant Interacting Langevin Dynamics for
                       Bayesian Inference},
     journal = {SIAM Journal on Applied Dynamical Systems},
     volume = {19},
     number = {3},
     pages = {1633--1658},
     year = {2020},
     url = {https://epubs.siam.org/doi/abs/10.1137/19M1304891},
     bibtex_show = {true},
     publisher = {SIAM},
     arxiv = {1912.02859}
   }

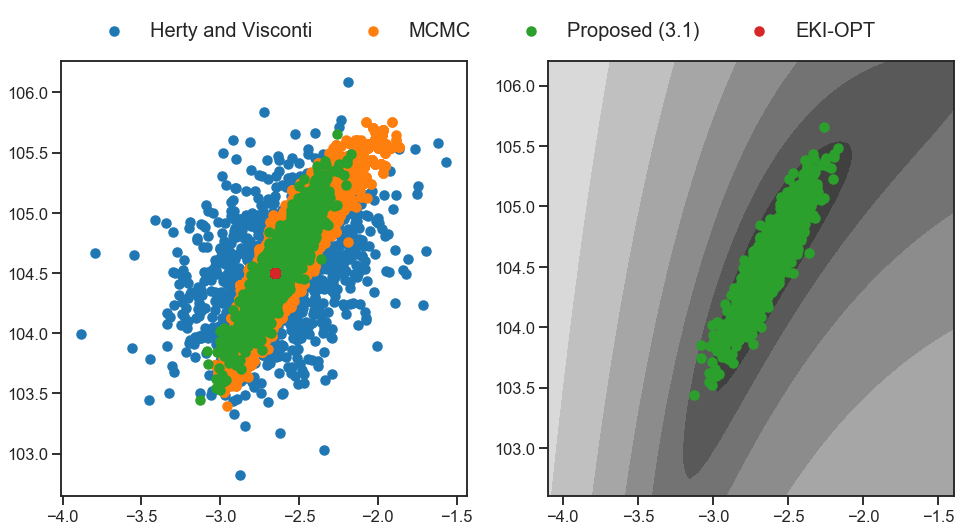
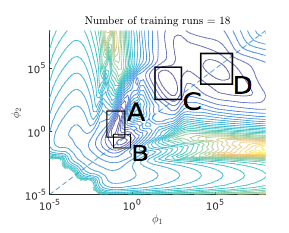
2. EKS

   

   Interacting Langevin Diffusions: Gradient Structure and Ensemble Kalman Sampler

   Garbuno-Inigo, Alfredo, Hoffmann, Franca, Li, Wuchen, and Stuart, Andrew M

   SIAM Journal on Applied Dynamical Systems 2020

   Abs arXiv Bib

   Solving inverse problems without the use of derivatives or adjoints of the forward model is highly desirable in many applications arising in science and engineering. In this paper we propose a new version of such a methodology, a framework for its analysis, and numerical evidence of the practicality of the method proposed. Our starting point is an ensemble of overdamped Langevin diffusions which interact through a single preconditioner computed as the empirical ensemble covariance. We demonstrate that the nonlinear Fokker–Planck equation arising from the mean-field limit of the associated stochastic differential equation (SDE) has a novel gradient flow structure, built on the Wasserstein metric and the covariance matrix of the noisy flow. Using this structure, we investigate large time properties of the Fokker–Planck equation, showing that its invariant measure coincides with that of a single Langevin diffusion, and demonstrating exponential convergence to the invariant measure in a number of settings. We introduce a new noisy variant on ensemble Kalman inversion (EKI) algorithms found from the original SDE by replacing exact gradients with ensemble differences; this defines the ensemble Kalman sampler (EKS). Numerical results are presented which demonstrate its efficacy as a derivative-free approximate sampler for the Bayesian posterior arising from inverse problems.

   @article{Garbuno-Inigo2021,
     author = {Garbuno-Inigo, Alfredo and Hoffmann, Franca and Li, Wuchen and Stuart, Andrew M},
     title = {Interacting Langevin Diffusions: Gradient Structure
                       and Ensemble Kalman Sampler},
     journal = {SIAM Journal on Applied Dynamical Systems},
     volume = {19},
     number = {1},
     pages = {412--441},
     year = {2020},
     image = {/assets/img/pubimg/numerics00.png},
     url = {https://epubs.siam.org/doi/abs/10.1137/19M1251655},
     abbr = {EKS},
     bibtex_show = {true},
     publisher = {SIAM},
     selected = {true},
     arxiv = {1903.08866}
   }

2018

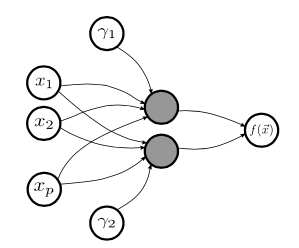
1. PhD Thesis

   

   Stochastic Methods for Emulation, Calibration and Reliability Analysis of Engineering Models

   Garbuno-Inigo, Alfredo,

   2018

   Abs Bib

   This dissertation examines the use of non-parametric Bayesian methods and advanced Monte Carlo algorithms for the emulation and reliability analysis of complex engineering computations. Firstly, the problem lies in the reduction of the computational cost of such models and the generation of posterior samples for the Gaussian Process’ (GP) hyperparameters. In a GP, as the flexibility of the mechanism to induce correlations among training points increases, the number of hyperparameters increases as well. This leads to multimodal posterior distributions. Typical variants of MCMC samplers are not designed to overcome multimodality. Maximum posterior estimates of hyperparameters, on the other hand, do not guarantee a global optimiser. This presents a challenge when emulating expensive simulators in light of small data. Thus, new MCMC algorithms are presented which allow the use of full Bayesian emulators by sampling from their respective multimodal posteriors. Secondly, in order for these complex models to be reliable, they need to be robustly calibrated to experimental data. History matching solves the calibration problem by discarding regions of input parameters space. This allows one to determine which configurations are likely to replicate the observed data. In particular, the GP surrogate model’s probabilistic statements are exploited, and the data assimilation process is improved. Thirdly, as sampling- based methods are increasingly being used in engineering, variants of sampling algorithms in other engineering tasks are studied, that is reliability-based methods. Several new algorithms to solve these three fundamental problems are proposed, developed and tested in both illustrative examples and industrial-scale models.

   @phdthesis{Garbuno-Inigo2018,
     author = {{Garbuno-Inigo, Alfredo}},
     image = {/assets/img/pubimg/04.png},
     abbr = {PhD Thesis},
     title = {{Stochastic Methods for Emulation, Calibration and
                       Reliability Analysis of Engineering Models }},
     url = {https://livrepository.liverpool.ac.uk/3026757/},
     bibtex_show = {true},
     school = {University of Liverpool},
     year = {2018}
   }

2017

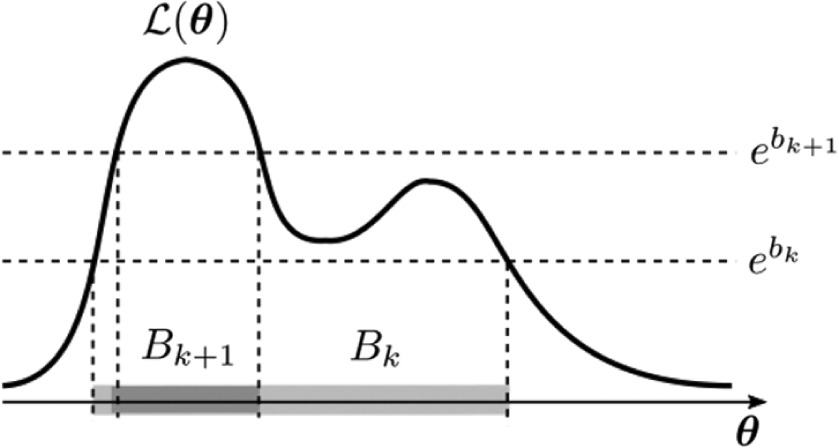
1. BUS

   

   Bayesian Updating and Model Class Selection With Subset Simulation

   DiazDelaO, FA, Garbuno-Inigo, A, Au, SK, and Yoshida, I

   Computer Methods in Applied Mechanics and Engineering 2017

   Abs Bib

   Identifying the parameters of a model and rating competitive models based on measured data has been among the most important but challenging topics in modern science and engineering, with great potential of application in structural system identification, updating and development of high fidelity models. These problems in principle can be tackled using a Bayesian probabilistic approach, where the parameters to be identified are treated as uncertain and their inference information are given in terms of their posterior (i.e., given data) probability distribution. For complex models encountered in applications, efficient computational tools robust to the number of uncertain parameters in the problem are required for computing the posterior statistics, which can generally be formulated as a multi-dimensional integral over the space of the uncertain parameters. Subset Simulation (SuS) has been developed for solving reliability problems involving complex systems and it is found to be robust to the number of uncertain parameters. An analogy has been recently established between a Bayesian updating problem and a reliability problem, which opens up the possibility of efficient solution by SuS. The formulation, called BUS (Bayesian Updating with Structural reliability methods), is based on conventional rejection principle. Its theoretical correctness and efficiency requires the prudent choice of a multiplier, which has remained an open question. Motivated by the choice of the multiplier and its philosophical role, this paper presents a study of BUS. The work leads to a revised formulation that resolves the issues regarding the multiplier so that SuS can be implemented without knowing the multiplier. Examples are presented to illustrate the theory and applications.

   @article{Diazdelao2017,
     author = {DiazDelaO, FA and Garbuno-Inigo, A and Au, SK and Yoshida, I},
     title = {Bayesian Updating and Model Class Selection With
                       Subset Simulation},
     journal = {Computer Methods in Applied Mechanics and
                       Engineering},
     volume = {317},
     pages = {1102--1121},
     year = {2017},
     abbr = {BUS},
     url = {http://www.sciencedirect.com/science/article/pii/S0045782516308283},
     bibtex_show = {true},
     publisher = {Elsevier},
     image = {/assets/img/pubimg/03.jpg}
   }

2016

1. 

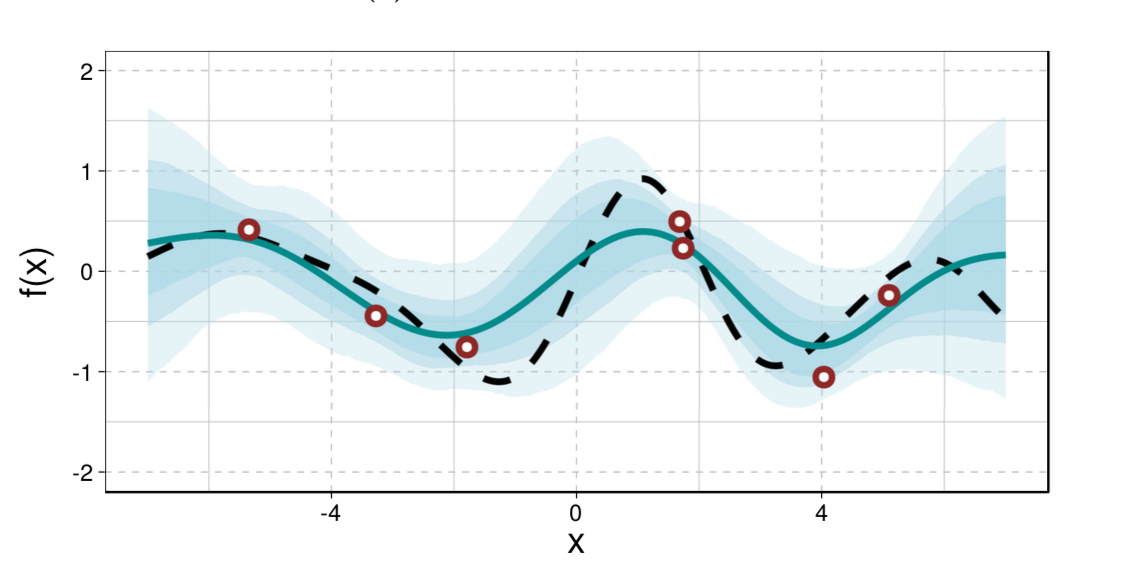
   Transitional Annealed Adaptive Slice Sampling for Gaussian Process Hyper-Parameter estimation

   Garbuno-Inigo, Alfredo, DiazDelaO, F. A., and Zuev, K. M.

   International Journal for Uncertainty Quantification 2016

   Abs Bib

   Surrogate models have become ubiquitous in science and engineering for their capability of emulating expensive computer codes, necessary to model and investigate complex phenomena. Bayesian emulators based on Gaussian processes adequately quantify the uncertainty that results from the cost of the original simulator, and thus the inability to evaluate it on the whole input space. However, it is common in the literature that only a partial Bayesian analysis is carried out, whereby the underlying hyper-parameters are estimated via gradient-free optimisation or genetic algorithms, to name a few methods. On the other hand, maximum a posteriori (MAP) estimation could discard important regions of the hyper-parameter space. In this paper, we carry out a more complete Bayesian inference, that combines Slice Sampling with some recently developed Sequential Monte Carlo samplers. The resulting algorithm improves the mixing in the sampling through delayed-rejection, the inclusion of an annealing scheme akin to Asymptotically Independent Markov Sampling and parallelisation via Transitional Markov Chain Monte Carlo. Examples related to the estimation of Gaussian process hyper-parameters are presented.

   @article{Garbuno-Inigo2016,
     title = {{Transitional Annealed Adaptive Slice Sampling for
                       Gaussian Process Hyper-Parameter estimation}},
     journal = {International Journal for Uncertainty
                       Quantification},
     volume = {6},
     number = {4},
     year = {2016},
     author = {Garbuno-Inigo, Alfredo and DiazDelaO, F.~A. and Zuev, K.~M.},
     file = {../assets/pdf/2015/taass.pdf},
     image = {/assets/img/pubimg/01.png},
     url = {http://www.dl.begellhouse.com/journals/52034eb04b657aea,55c0c92f02169163,2f3449c01b48b322.html},
     bibtex_show = {true},
     publisher = {Begel House Inc.}
   }

2. 

   Gaussian Process Hyper-Parameter Estimation Using Parallel Asymptotically Independent Markov Sampling

   Garbuno-Inigo, A., DiazDelaO, F. A., and Zuev, K. M.

   Computational Statistics & Data Analysis 2016

   Abs Bib

   Gaussian process emulators of computationally expensive computer codes provide fast statistical approximations to model physical processes. The training of these surrogates depends on the set of design points chosen to run the simulator. Due to computational cost, such training set is bound to be limited and quantifying the resulting uncertainty in the hyper-parameters of the emulator by uni-modal distributions is likely to induce bias. In order to quantify this uncertainty, this paper proposes a computationally efficient sampler based on an extension of Asymptotically Independent Markov Sampling, a recently developed algorithm for Bayesian inference. Structural uncertainty of the emulator is obtained as a by-product of the Bayesian treatment of the hyper-parameters. Additionally, the user can choose to perform stochastic optimisation to sample from a neighbourhood of the Maximum a Posteriori estimate, even in the presence of multimodality. Model uncertainty is also acknowledged through numerical stabilisation measures by including a nugget term in the formulation of the probability model. The efficiency of the proposed sampler is illustrated in examples where multi-modal distributions are encountered.

   @article{Garbuno-Inigo2017,
     title = {{Gaussian Process Hyper-Parameter Estimation Using
                       Parallel Asymptotically Independent Markov Sampling
                       }},
     author = {Garbuno-Inigo, A. and DiazDelaO, F.~A. and Zuev, K.~M.},
     issn = {0167-9473},
     journal = {Computational Statistics \& Data Analysis },
     keywords = {Gaussian process},
     pages = {367 - 383},
     url = {http://www.sciencedirect.com/science/article/pii/S0167947316301311},
     volume = {103},
     year = {2016},
     bibtex_show = {true},
     file = {../assets/pdf/2015/paims.pdf},
     image = {/assets/img/pubimg/02.png}
   }